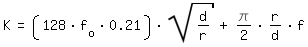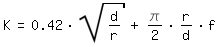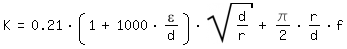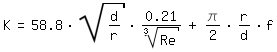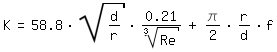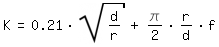Perte de charge sur des coudes

Δ p = K · ρ/2 · v2
Δ p	: Perte de charge d´un coude 90º
K	: Coefficient de résistance (Coefficient de frottement) d´un coude 90º
ρ	: Densité
v	: Vitesse moyenne dans le tube
Re	: nombre de Reynolds Re = ρ · v · d / η
μ	: Viscosité Dyn.
d	: Diamètre intérieur du coude

Le Coefficient de résistance dans les coudes dépend du Re (nombre de Reynolds), de la rugosité des parois et de la géométrie des coueds. La perturbation d´écoulement produite par un coude sur un tuyau influence l´écoulement en amont et en aval du coude. La perte de charge dans la série des coudes connectées est plus petite ou égale à la multiplication de celle d´un coude unique. On part de l´hypothèse que les diamètres intérieurs du coude et du tuyau sont égaux.

Pour Re < 2320 (écoulement laminaire) le Coefficient de résistance est selon [Ghia 1977, page 648]. Le graphique mentionné par Ghia est approché comme suit:

K / Kp = 0.026 · Dean ^0.661 +1
Kp	= π/2 · r/d · 64/Re		Coefficient de résistance d´un tube droit quel longueur est égale à la ligne médiane de coude
Dean	= Re · (d/r)^0.5		nombre de Dean
r			Rayon de la ligne médiane du coude

Pour Re > 2320 (zone de transition et écoulement turbulent) l´approche de [Krüger 1970, page 39 ff] est utilisée. Krüger tient compte de l´influence du rayon de courbure et de la rugosité sur la perte de charge d´un coude.

ε /d		2320 < Re < 2 x 10^5	Re > 2 x 10^5
> 0.001
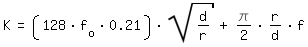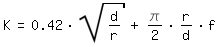< 0.001	Re > Re*
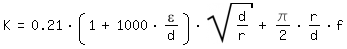	Re < Re*
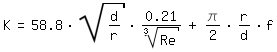0

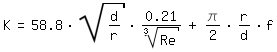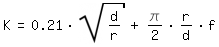f	: Facteur de friction de Darcy-Weisbach d´un tube droit
f,o	: Facteur de friction de Darcy-Weisbach d´un tube droit et lisse
ε	: Rugosité
Re* = (2,89/(1+1000 x ε /d))^12

K = f(Re)

Littérature

[Ghia 1977] K.N. Ghia, J.S. Sokhey, Laminar Incompressible Viscous Flow in Curved Ducts of Regular Cross-Sections, Transactions of the ASME Journal of Fluids Engineering, December 1977, page 640 ff

[Kittredge 1957] C.P. Kittredge, D.S. Rowley, Resistance Coefficients for Laminar and Turbulent Flow Through One-Half-Inch Valves and Fittngs, Transactions of the American Society of Mechanical Engineering ASME, Volume 79 January 1957, Fig. 6

[Krüger 1970] H. Krüger, Berechnung strömungstechnischer Kennwerte von Durchströmteilen für Flüssigkeiten und Gase, Mitteilungen des Institut für Leichtbau und ökonomische Verwendug von Werkstoffen, IfL- Mitteilungen, Dresden 1970, Beilage

[Miller 2008] D.S. Miller, Internal Flow Systems, 2nd Edition 2008, Miller Innovations Bredford UK, page 223 f

[Ward Smith 1980] A.J. Ward-Smith, The fluid dynamics of flow in pipes and ducts, Clarendon Press, Oxford 1980, pages 248-268

[White 1929] C.M. White, Streamline flow through curvd pipes. Proc. Royal Soc., London, 123 (1929), page 645, cited by [Krüger 1970, page 39]