Écoulement turbulent
| Le diamètre hydraulique
dH est choisi de sorte que la perte de charge et le débit
moyen dans le tuyau rond entièrement rempli avec dH
et dans la section transversale non circulaire soient égales. Le débit
volumétrique doit être calculé: | ||||||||||||||
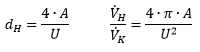 | A: section transversale non circulaire U: périmètre non circulaire | |||||||||||||
| canal rectangulaire: | ||||||||||||||
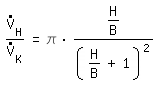 | 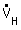 : débit volumétrique dans le tube avec
dH : débit volumétrique dans le tube avec
dH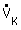 : débit volumétrique dans le
canal rectangulaire : débit volumétrique dans le
canal rectangulaireH : hauteur du canal B : largeur du canal | |||||||||||||
| ||||||||||||||
Écoulement laminaire
| Le diamètre hydraulique dH peut être estimé pour les sections transversales sélectionées de manière à ce que la perte de charge et le débit dans le tuyau rond complètement rempli avec dH et dans la section transversale non circulaire soient égales. | ||||||||||||||
| canal rectangulaire: | ||||||||||||||
| dH = H · f (H/B) | H: hauteur du canal B: largeur du canal, B > H f(H/B): dérivation voir ci-dessous | |||||||||||||
| ||||||||||||||
Théorie
Écoulement turbulent En écoulement turbulent on choisit le diamètre hydraulique du tuyau de remplacement de sorte que la contrainte au cisaillement sur la paroi τw et la perte de charge Δp du tuyau de remplacement soient égales à la contrainte au cisaillement sur la paroi et à la perte de charge de la conduite non circulaire. Et ainsi cela s´applique pour équilibrer les forces sur le tuyau de remplacement et la conduite non circulaire:
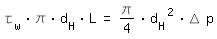 |
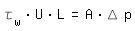 |
L: Longueur |
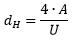 | ||
Avec la même vitesse, il se crée dans le tuyau entièrement rempli avec le diamètre hydraulique dH la même chute de pression que dans la section transversale non circulaire. Le rapport entre la contrainte moyenne au cisaillement sur la paroi et la vitesse d´écoulement moyenne est approximativement identique, étant donné que la courbe de distribution des vitesses en écoulement turbulent est très plate.
Les débits doivent être calculés. Avec la même vitesse ecrivez nous:
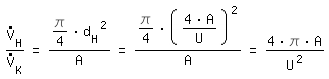
canal rectangulaire:
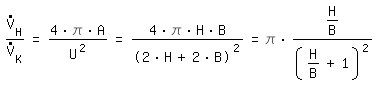
Écoulement laminaire
En écoulement laminaire il existe de bonnes formules approchées pour de nombreuses sections transversales avec le débit comme fonction de la perte de charge. [Berker 1963] résume les solutions fermées pour la distribution des vitesses d´écoulement laminaire dans diverses sections transversales.
Pour une conduite rectangulaire avec les dimensions BxH, cela s´appliques avec B>H:
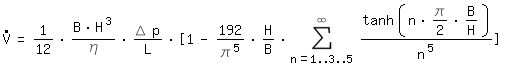
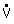 : Débit volumétrique
η: Viscosité Dyn.
L: longueur du canal
: Débit volumétrique
η: Viscosité Dyn.
L: longueur du canalPour B>>H, cette équation converge vers la solution pour deux plaques parallèles, également nommée écoulement de Couette (pour la dérivation voir annexe):
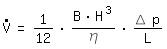
Le diamétre hydraulique est obtenu de la manière suivante:
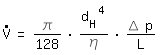 |
écoulement laminaire dans un tube (Hagen Poiseuille) (pour la dérivation voir annexe) | |
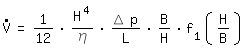 |
écoulement laminaire dans un canal rectangulaire |
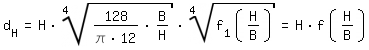
 |
| Hagen Poiseuille and Couette Flow |
| Littérature |
| [Berker 1963] Tapis Berker, Encyclopedia Of Physics / Handbuch der Physik, Edited by S. Flügge, Springer-Verlag 1963, page 70 |